Introduction

Union find is a data structure that can be used to efficiently keep track of whether two objects are connected or not. It allows you to quickly merge two subsets into a single subset, and efficiently determine whether two elements belong to the same subset.

It performs 2 basic operations: 1) union:- connect 2 objects 2) connected:- check whether 2 objects are connected

For example:- If 0 is connected with 1 and 1 is connected with 2, then we check whether 0 and 2 are connected. The output that we get is true.

Let's Implement this Data Structure in Java

1) Initialise a UnionFind class that will contain the following methods inside

public class UnionFind{
    int[] size; //size of tree
    int[] id; //id of objects
    UnionFind(int n){}
    private int find(int i){}
    public boolean connected(int p,int q){}
    public void union(int p,int q){}
}

Let me explain to you the working of each method and then we are going to implement them one by one starting from their constructor.

We have two arrays, one is the size and the other is the id. The constructor initializes the array of n size. Find method finds the root of the node. The connected method tells whether two objects are connected. The union method connects the two objects.

2) Implement the constructor

    UnionFind(int n){
        id=new int[n];
        size=new int[n];
        for(int i=0;i<n;i++){
            id[i]=i;
        }
    }

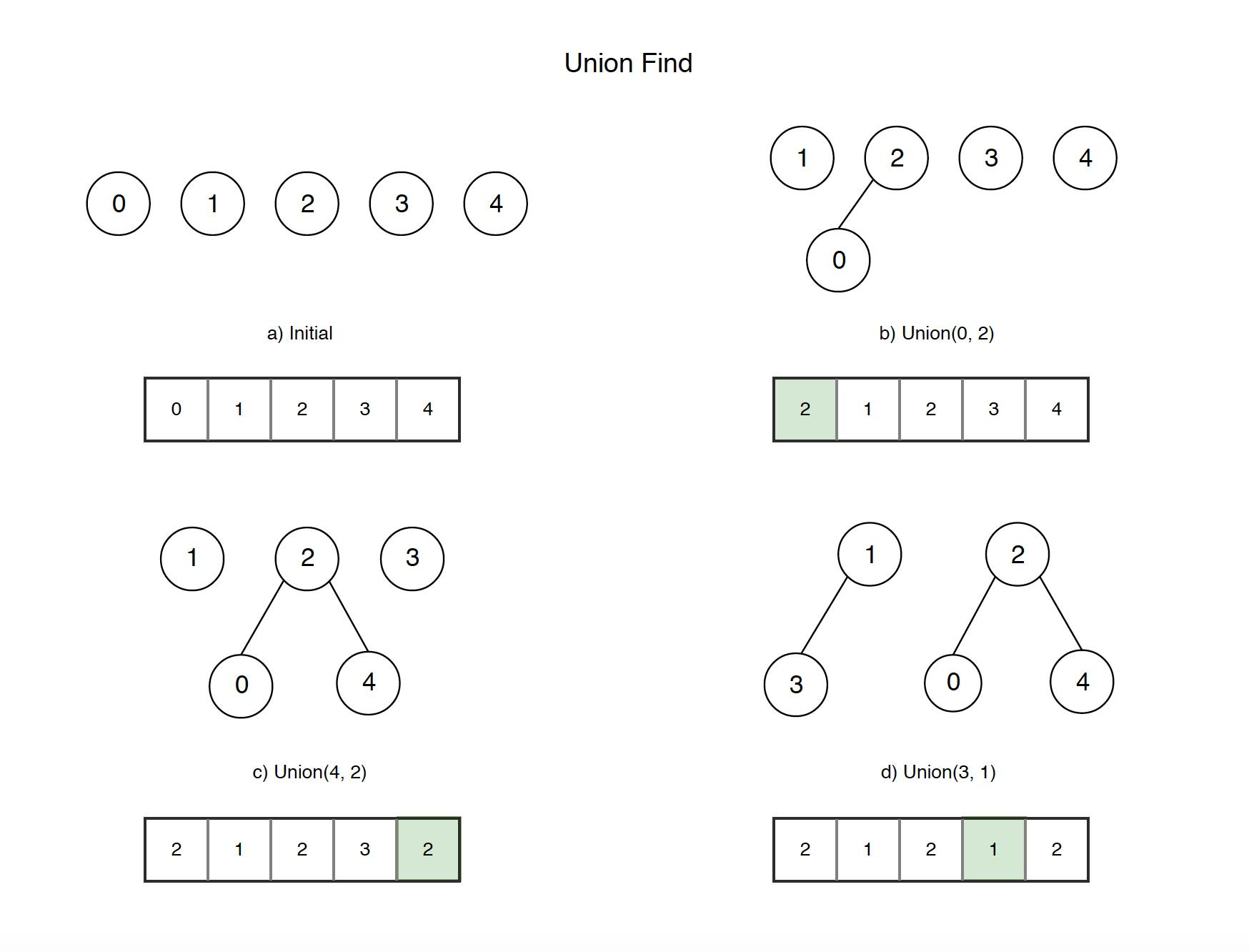
The constructor initializes the id and size array to n size and stores values from 0 to n-1 in the id array. The arrays look something like this

Here size arrays tell the size of a tree i.e number of rows present in a tree.

3) Implement the find method

    private int find(int i){
        while(i!=id[i]){
            id[i]=id[id[i]];    //make every node in the path points to it's      grandparent [Flatten the tree and reduce the cost of finding]
            i=id[i]; //moving to parent
        }
        return i;
    }

This method finds the root of the node and is the helping method for implementing the connected and union method. We change the current node to its parent node with i=id[i] until i!=id[i] i.e current node is not equal to its index (means root node).

id[i]=id[id[i]] This inline code snippet is optional but using it reduces the complexity further and it does it by attaching the current sub-tree to its grand-parent which reduces the size of the tree while finding it again.

4) Implementing a connected method

public boolean connected(int p,int q){
        return find(p)==find(q);
    }

This method is used to find whether p and q nodes are connected. This method simply checks whether the root node of the node p matches with the root node of the node q .It does it by using a method find which gives the root node.

5) Implement a union method

    public void union(int p,int q){
        int P=find(p); //root of P
        int Q=find(q); // root of Q
        if(connected(P, Q)) return; //already connected
        //Connecting based on size of tree
        if(size[P]<size[Q]){
            id[P]=Q;
            size[Q]+=size[P];
        }else{
            id[Q]=P;
            size[P]+=size[Q];
        }
    }

This method takes the root node of both p and q using the find method and stores them in P and Q respectively. Then using the connected method to check whether the nodes are already connected or not. After that, we compare the size of root nodes P and Q using a size array and a smaller tree is attached to the larger tree.

After doing all the above steps, our whole code looks something like this

public class UnionFind{
    int[] size; //size of tree
    int[] id; //id of objects
    UnionFind(int n){
        id=new int[n];
        size=new int[n];
        for(int i=0;i<n;i++){
            id[i]=i;
        }
    }
    private int find(int i){
        while(i!=id[i]){
            id[i]=id[id[i]];    //make every node in the path points to it's grandparent [Flatten the tree and reduce the cost of finding]
            i=id[i]; //moving to parent
        }
        return i;
    }
    public boolean connected(int p,int q){
        return find(p)==find(q);
    }
    public void union(int p,int q){
        int P=find(p); //root of P
        int Q=find(q); // root of Q
        if(connected(P, Q)) return; //already connected
        //Connecting based on size of tree
        if(size[P]<size[Q]){
            id[P]=Q;
            size[Q]+=size[P];
        }else{
            id[Q]=P;
            size[P]+=size[Q];
        }
    }
    public static void main(String[] args) {
        UnionFind uf=new UnionFind(9);
        uf.union(0, 1);
        uf.union(1, 2);
        System.out.println(uf.connected(0, 2));
    }
}

In this main method, we simply connect nodes 0 and 1, 1 and 2. After that, we check whether 0 and 2 are connected. The output that we get gives true.

Working Image of this data structure

Reason to learn union-find data structure

1) Dynamic connectivity

Union find can be used to efficiently determine whether two elements are connected in a dynamic set of elements, where elements may be added or removed over time.

2) Percolation

Percolation is a model used to study the behavior of systems that exhibit a transition between an ordered and a disordered state, such as the flow of fluids through a porous material. Union-Find is used to determine whether the fluid flow in the n*n grid matrix from top to bottom.

3) Kruskal's algorithms

Kruskal's algorithm for finding the minimum spanning tree of a graph: Union find is used to keep track of the connected components of the graph, and to efficiently merge them as edges are added to the tree.

4) Network flow algorithms

Union find is used to identify the connected components of a flow network, and to efficiently merge them as flow is added to the network.

5)Tarjan's algorithm

Tarjan's algorithm for finding the strongly connected components of a graph: Union find is used to efficiently identify the strongly connected components of a graph, which are sets of vertices that are strongly connected by directed edges.

6) Computational geometry

Union find can be used to efficiently perform operations such as intersection and union of geometric shapes.

7) Software engineering

Union find can be used to identify connected components in software systems, such as classes or modules that depend on each other.

8) Image processing

Union find can be used to identify and label connected components in images, such as objects in a photograph or text in a scanned document.